As as very wise person once quipped:
Homeowners live in the monthly payments, not the purchase price.
Mortgage interest rates are undoubtedly and understandably a large consideration when it comes to purchasing a new home. Over the past several years we have experienced historically low mortgage interest rates as the U.S. economy slowly recovered from the 2008 financial crisis. In fact, since October 2011 30-year fixed-rate mortgages have been below 4% for the most part, a far cry from October of 1981 when rates were a whopping 17%.
That said, despite whether rates are relatively low or high, when interest rates rise buyers feel they are paying more for their home. Often buyers respond to a 1/4 or 1/2 point increase in interest rates by reducing their price point, or by putting the purchase on hold altogether in hopes that rates will fall in the future.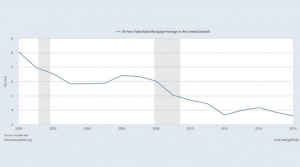
Want my advice? Before we drastically change course, or decide to continue renting for another year or two, let’s calculate how that increase actually affects our purchase in real dollars to make sure we make the best and most rational decision possible. We will work it out together…
For the purposes of this exercise, we will use the current conventional 30-year fixed-rate mortgage interest rate of 4.125% and compare it to the average rate from this time last year which was about 3.625% – a difference of 1/2 or .5 of a point. So, how does that .5 change in mortgage interest rate impact us, and how can we put it into terms which will help us with our rent vs. buy calculation? Since there will be a true financial cost to a higher rate, it’s best to use dollars rather than decimals by calculating our exact monthly mortgage payment (which consists of both principle and interest, also known as “P & I”) for both rates.
For you math fans out there, the equation to figure out your monthly payments looks like this:
M = L[c (1 + c)n] / [(1+c)n – 1]
 Unfortunately, most of you are NOT math fans and would rather not try to figure out what L represents, let alone 1+c and n-1, which is why many of us end the exercise here. Well, I have great news for all you arithmophobes out there! There is a tool created by your math-loving buddies called a “mortgage amortization factor chart“, and it may help stop your head from spinning with painful memories of brackets, balancing equations and high school Calculus.
Unfortunately, most of you are NOT math fans and would rather not try to figure out what L represents, let alone 1+c and n-1, which is why many of us end the exercise here. Well, I have great news for all you arithmophobes out there! There is a tool created by your math-loving buddies called a “mortgage amortization factor chart“, and it may help stop your head from spinning with painful memories of brackets, balancing equations and high school Calculus.
The mortgage amortization factor chart does most of the heavy lifting for us by charting exactly what our monthly mortgage payment will be per $1000 borrowed, for several different mortgage terms. The first row (horizontal) is the mortgage term, and the first column (vertical) is the mortgage interest rate. Simply scroll down the “Rate” column until you find your rate, then follow that row right to the correct mortgage term (see mortgage amortization factor table below). For example, the mortgage amortization factor for a 3.625% interest rate on a 30-year fixed-rate mortgage is 4.56. How does that translate into dollars? …EASY! The table shows us that for every $1000 you borrow, you will pay $4.56 per month for 30 years (or until you sell the apartment or refinance your loan – both of which are far more likely than living out the entire term of the loan in that apartment).
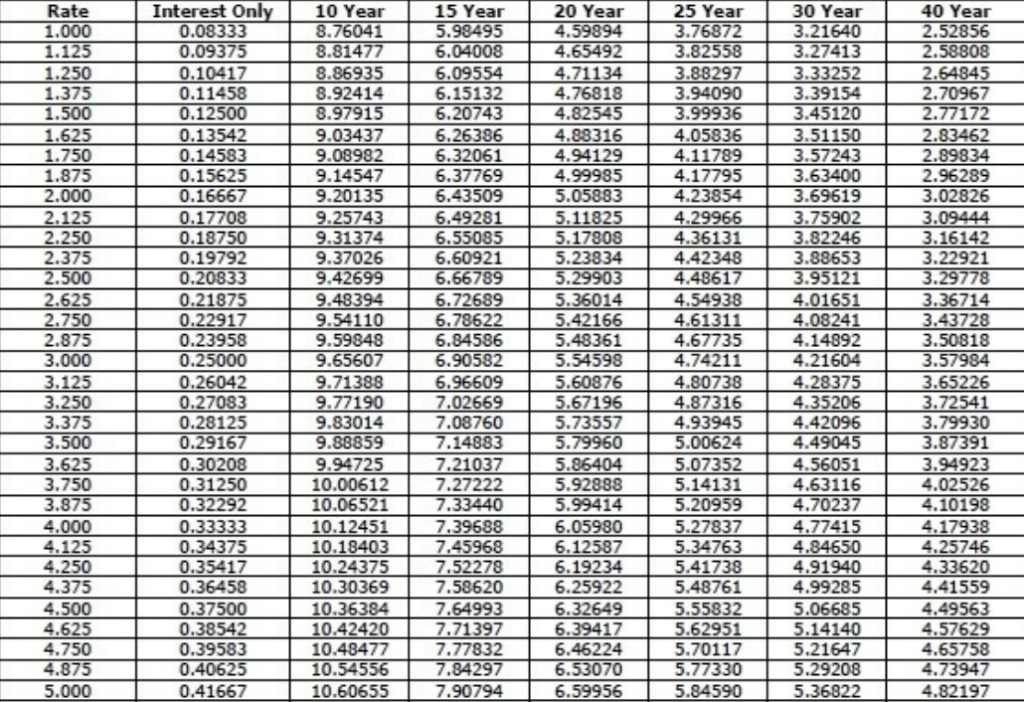 Of course, calculating our mortgage payment in $1000 increments doesn’t make a lot of sense unless we are buying property in Iowa in the 1830s. Therefore, I like to use $100,000 increments which (thankfully) is an easy change to make. All we have to do is move the decimal point to the right two places – from $4.5600 to $456.00. So, each $100,000 I borrow will cost me $456 per month for 30 years.
Of course, calculating our mortgage payment in $1000 increments doesn’t make a lot of sense unless we are buying property in Iowa in the 1830s. Therefore, I like to use $100,000 increments which (thankfully) is an easy change to make. All we have to do is move the decimal point to the right two places – from $4.5600 to $456.00. So, each $100,000 I borrow will cost me $456 per month for 30 years.
Now that we have discovered a quick and easy way to calculate our monthly mortgage payment courtesy of those who like math, let’s figure out how the change in rate will affect us in real dollars by comparing our rates of 3.625% and 4.125% – a difference of 1/2 of a point or .5%. Using our mortgage factor table we know the following:
3.625% interest rate = $4.56 per $1000 borrowed
4.125% interest rate = $4.85 per $1000 borrowed
The difference between the two mortgage factors is .29 (4.85 – 4.56 = .29). Move the decimal over two spots and you get 29. So, for every $100,000 you borrow you are paying an extra $29 per month for you monthly mortgage payment. If you are purchasing a $1,000,000 apartment and plan to finance 80% of the purchase ($800,000) you will pay an additional $232/month (8 x 29 = 232). Now, that is certainly not insignificant, but let’s try to add some perspective when it comes to the overall deal, and why a 1/2 of a point jump in rates – or even 1% jump – should not necessarily dissuade you from purchasing an apartment. Here are four points to consider:
- As I mentioned, $232 is not an insignificant amount – especially on a monthly basis. That is nearly $2800/year after all. However, keep in mind that the overall mortgage payment on a loan of $800,000 at a 3.625% interest rate is $3648/month (456 x 8 = 3,648). Add a hypothetical (but very “reasonable”) maintenance payment of $1500/month and our total monthly (pre-tax) carrying cost figure is $5,148/month. Suddenly $232 (4.5% of the total monthly carrying costs) seems a little less significant in the overall picture.
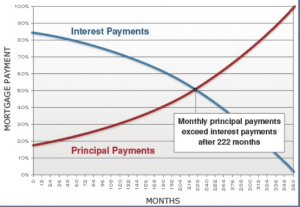 One of the biggest benefits of owning rather than renting is the tax deductibility of your monthly carrying costs, including the interest component of your mortgage payment. Although the relationship between principle and interest changes as you pay off the loan (see mortgage payment graph), for the first several years of the loan you will benefit from a high level of tax deductibility (75%-ish). So, how long you tend to own the apartment should be a large part of your calculation. Do do quick math on how the tax deductiblity will change the $232 number, multiply 232 x 12 ($2784) x 75% (or .75) = $2,088. $2.088 of that yearly 1/2 addition in rate in our example is tax deductible. Assuming a 30% tax bracket, you will save $626 each year or $52/month. So, $232/month is actually about $180/month!
One of the biggest benefits of owning rather than renting is the tax deductibility of your monthly carrying costs, including the interest component of your mortgage payment. Although the relationship between principle and interest changes as you pay off the loan (see mortgage payment graph), for the first several years of the loan you will benefit from a high level of tax deductibility (75%-ish). So, how long you tend to own the apartment should be a large part of your calculation. Do do quick math on how the tax deductiblity will change the $232 number, multiply 232 x 12 ($2784) x 75% (or .75) = $2,088. $2.088 of that yearly 1/2 addition in rate in our example is tax deductible. Assuming a 30% tax bracket, you will save $626 each year or $52/month. So, $232/month is actually about $180/month!- It is important to ask yourself how long you realistically plan to own the apartment. Do you see yourself selling in 5 years? 10? Let’s take a conservative approach and assume you will hold the apartment for 15 years. As we established above, the after-tax monthly burden of an extra .5% in interest rate on an $800,000 mortgage is roughly $180/month. Therefore, the “cost” of that rate increase over the 15 years of ownership is $32,400 ((180 x 12) x 15). That’s just over 3% of the entire purchase price and doesn’t begin to take into consideration the potential appreciation of the property over the next 15 years.
- We don’t live or purchase “in a vacuum”. If you are going to live in NYC – and don’t have the benefit of rent control or a wealthy family member – you are destined to either rent an apartment or own one. So, despite the fact that rates are higher than they were last year and last month, they are still at historic lows. The “rent vs. buy” calculation still favors buying if you have a) the down payment and post-closing reserves necessary to purchase, b) have the time to complete a purchase without becoming homeless and confused and c) plan to hold the property for more than just a few years (to allow for appreciation and mitigate the frictional costs of purchasing and selling (closing costs, etc.)).
At the end of the day, whatever you decide to do in response to increasing rates, do so with a clear understanding of what it mean in terms of dollars, not decimals. It will help you put the rate increase into perspective and allow you to make a rational decision, not a rash one.
_________________________________________________________________________
My name is Eirik Davey-Gislason and I work in real estate in New York City. This blog is an opportunity for me to educate everyone who has a horror story or is on the verge of one. By sharing, preparing and advising my audience on what to expect, what is normal, what is right, and what is wrong, I hope to do my part to expose the wrong-doers and shape the future of this dysfunctional thing we call NYC Real Estate.


